
| 2012年08月 十和田湖、奥入瀬サイクリング |
■ホームへ | |
| ↑上のページへ | ||
| ラン実施日 | 2012年08月11日(土) |
|---|---|
| コース概略 | 二戸市 → 田子町 → 十和田湖~奥入瀬渓流 → 十和田町 → 五戸 → 三戸 → 二戸 (166km) |
| 天候 | 快晴 |
今年の5月に佐渡ロングライドに参加してから、ロングライドの面白さに目覚めてしまいました。どうやらこういう走り方は自分の性分に合っているみたいです。
とはいえなかなかまとまって走れず数ヶ月が経過。やっとお盆休みを利用して走ることができました。
僕の実家は岩手と青森の境に有ります。お盆休みには5日間ほど帰省していました。そこから十和田湖を経由して戻ってくるコースはざっとこんな感じです。
距離は約160km、最大標高差は668m。今の自分の体力で考えるとちょっと山道がきつそうですが、まあ一日もあればなんとか走り切れるでしょう。
途中の山道、十和田湖や、奥入瀬の景色を眺めながらのんびり走ろうと思います。
朝6:30に実家を出発。
今から越えようとしている山の空には多少靄が見えています。けれど天気予報によると、じきに晴れるようです。雲間からの陽も気持ち良く出発します。
家から出て2kmほど行くと「いわて銀河鉄道線」の斗米(とまい)駅が在ります。ここを越えて県道32号線に乗れば、あとはずーっと道なりに進んでいくだけで十和田湖に着きます。判りやすいコースです。
ひと山越えると青森県田子町。にんにく好きの方なら御存じかもしれません。最近ここはブランドにんにくの産地として名が知られるようになりました。町中でもそれをアピールしたポスターなどが目につきます。
そして市街地を過ぎると山道に入ります。

晴れました。
気分も浮かれようというものです。頭の中で「ピクニック」の曲が流れていました(「♪丘を越え行こうよ♪」ってやつです)。
ただ、この写真を撮影した地点(十和田湖まで25km)から先が、この日最大の難関でした。平均斜度 6% で 7km 程走るのですが、途中何度も休んでしまいました。
鈍ってるなあ、自分の身体。

そして迷ヶ平(まよがたい - 下図矢印位置)を越えて、高山を下ると十和田湖に着きます。
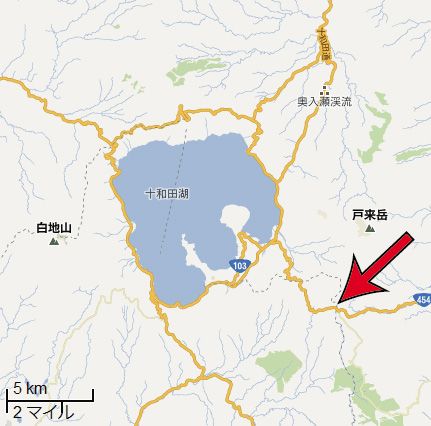
この高山から十和田湖までの下りは本日のコースの中で最も厳しい下り傾斜です(下図矢印位置)。最大 -10% で 2km ほど続くのですが、ここで少し怖い思いをしました。
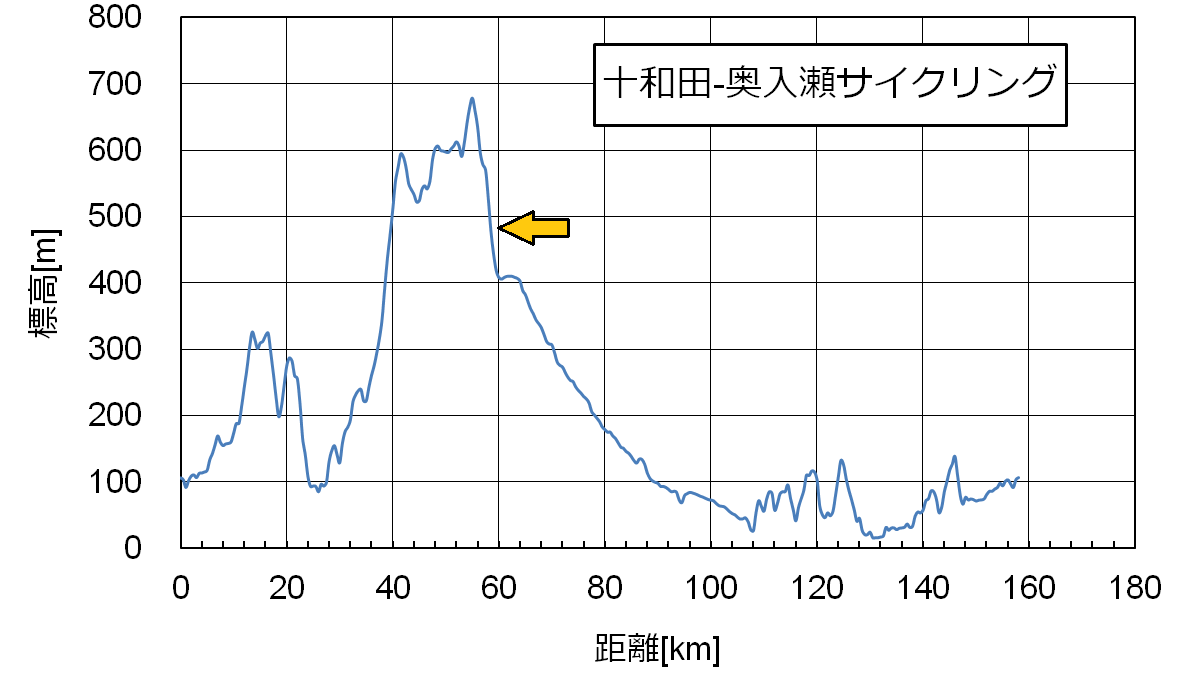
いつものようにリアブレーキを主に使いながら下って行ったところ、途中でブレーキの手応えが急に軽くなったんです。
直感的に「ブレーキワイヤーに何かが起きた」と思い、主ブレーキをリアからフロントに切り替え、徐々に減速・停止しブレーキ状態を確認したところ、案の定ブレーキワイヤーが抜けかけていました。


上図左はフロントブレーキ。こちらは正常で、ブレーキワイヤがちゃんと繋がれています。一方で右はリアブレーキの状態。ワイヤ先端が抜け落ちて、ぎりぎりカンチブレーキのアーム部分に引っ掛かっていることが判ります。
ブレーキワイヤのつなぎ直しをしようかとも思ったのですが、このようにワイヤに余分の無い状態ですからどうしようも有りません。仕方がないのでここから先はフロントブレーキ主体で、スピードを出さずに坂を下りる事にしました。
そして間もなく十和田湖に到着しました。
あいにく十和田湖に着いたら曇り空で、なかなか良い写真が撮れません。ちょっとズルですが、以下の写真は Wikipedia から引用しました。天気が良ければこのような景色に出会えます。

十和田湖畔で昼飯に菓子パンなど食べていたところ、自転車ツーリングをしている学生さんに出会いました。話を聞くと、名古屋から北海道の宗谷岬を目指して旅行中とのこと。少し自転車話などして別れました。
あのあと彼は無事宗谷に着いたかなあ。名前も聞かなかったけど気になります。もしもこのホームページを見たら連絡ください。8月11日に十和田湖畔で出会ったおっさんです。黄色いサイクルジャージ着てました。
さて、その後、奥入瀬を走ります。

奥入瀬渓流は林の中を流れる清浄な印象で、場所によって流れが急だったりゆるやかだったりといくつかの表情を見せてくれます。上の写真を撮ったのは銚子大滝の手前くらいだったかな。涼しく綺麗な緑でした。
けれど正直なところ、ここはサイクリングで立ち寄るのには向いていないように思えます。特に、今回のように十和田湖から渓流に沿った下りを走るとあっという間に通り過ぎてしまいます。これでは折角の景色が楽しめません。なので個人的にはここには徒歩で行き、遊歩道をゆっくりと散策する方が良いような気がしました。
ちなみに帰宅後、ウチの親に奥入瀬渓流の印象を伝えたところ「観光地化が進むにつれて、景色の迫力が無くなってきた」というコメントを受けました。なんでも母が女学生の頃(60年以上も前!)、奥入瀬は原生林と言って良いような状態で、人の背丈ほどもある羊歯が茂ったりしていたそうです。「恐竜が出てきてもおかしくないような場所だったのに」と言われると空想が膨らみます。それは見てみたかったなあ。確かに今の林にはそこまでの迫力は有りません。
一例と言えるかどうか判りませんが、この日奥入瀬を走っていたら道路は多くの車で混雑していました。観光名所となっている滝の近くなどでは路上駐車が横行していて、渓谷の清冽な印象が瞬時に白けたりもします。
とはいえ、観光地化が進み、道路が整備されてきたおかげで自分も気楽に自転車で十和田奥入瀬まで辿りつけたのも事実です。
複雑な心境です。善し悪しだなと思いました。

その後、十和田湖町を経由して、国道4号線を南下し二戸に戻ります。
下の写真は青森県三戸町の名久井岳。僕のお気に入りの山の一つです。標高 615m 程度の小さい山ではありますが、なんか形と雰囲気が良いんです。神様が座られるのに相応しい印象を受けます。
サイクリング後半の草臥れた気分を癒してくれました。
今度いつか、ここを上ってみようと思います。

そして夕方18時過ぎに帰宅。結果は 12 時間掛かって走行距離は 160km 強。平均時速は 14km/h を割ってます。
ロングライドは平均時速 20km/h が一つの目安ですから、こんなんじゃ全っ然ダメです。もっともっと精進せねばと思いました。
頑張らねば。
青森から秋田の県境を走っていた時のことである。
山路を登りながら、こう考えた。
とかくに人の世は住みにくい。
...というのは冗談で、考えてたのは、コースの事です。
今回のサイクリングは、ロングライドの練習を意識していました。今年の五月に佐渡ロングライドというイベントに参加して以降、がぜんロングライドに興味を持ったのですが、さてどういうコースで練習したら良いのか良く判りません。
今回の十和田湖、奥入瀬コースにしても「なんとなく良さそう」という観点で選んだのですが、果たしてこれは良い練習になっているんでしょうか。たとえば佐渡のコースと比べてみて、どんなもんなんでしょう。
というか。大体にして「コースの比較」って、どうしたらいいもんなんでしょう。
コース比較でよく聞くのは
という方法です。
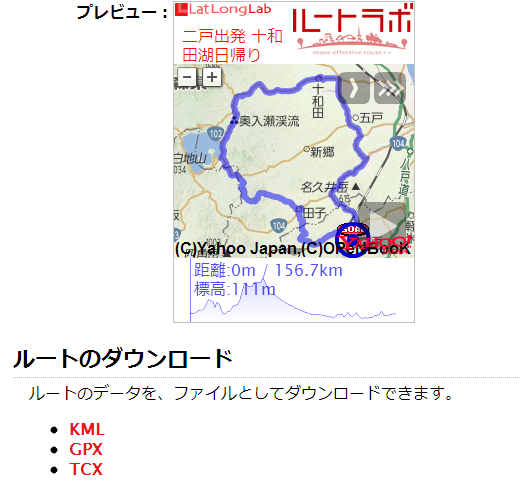
これは皆さま御存じの「ルートラボ(http://latlonglab.yahoo.co.jp/route/)」を利用すれば、すぐに判ります。下図に示すように、総走行距離から最大標高差、平均斜度なり一目で示してくれます。
そして今回のコースを佐渡ロングライドコースと比較すると、こうなります。
| 今回のコース | 佐渡ロングライド 210kmコース |
佐渡に対する 今回のコースの比率 |
|
|---|---|---|---|
| 距離 | 156.7 km | 204.1km | 77% |
| 平均斜度 | 全体 : 0% 上り : 4.1% 下り : 3.8% |
全体 : 0% 上り : 4.1% 下り : 3.9% |
全体 : - 上り : 100% 下り : 97% |
| 獲得標高 | 上り : 2020m 下り : 1968m |
上り : 2612m 下り : 2623m |
上り : 77% 下り : 75% |
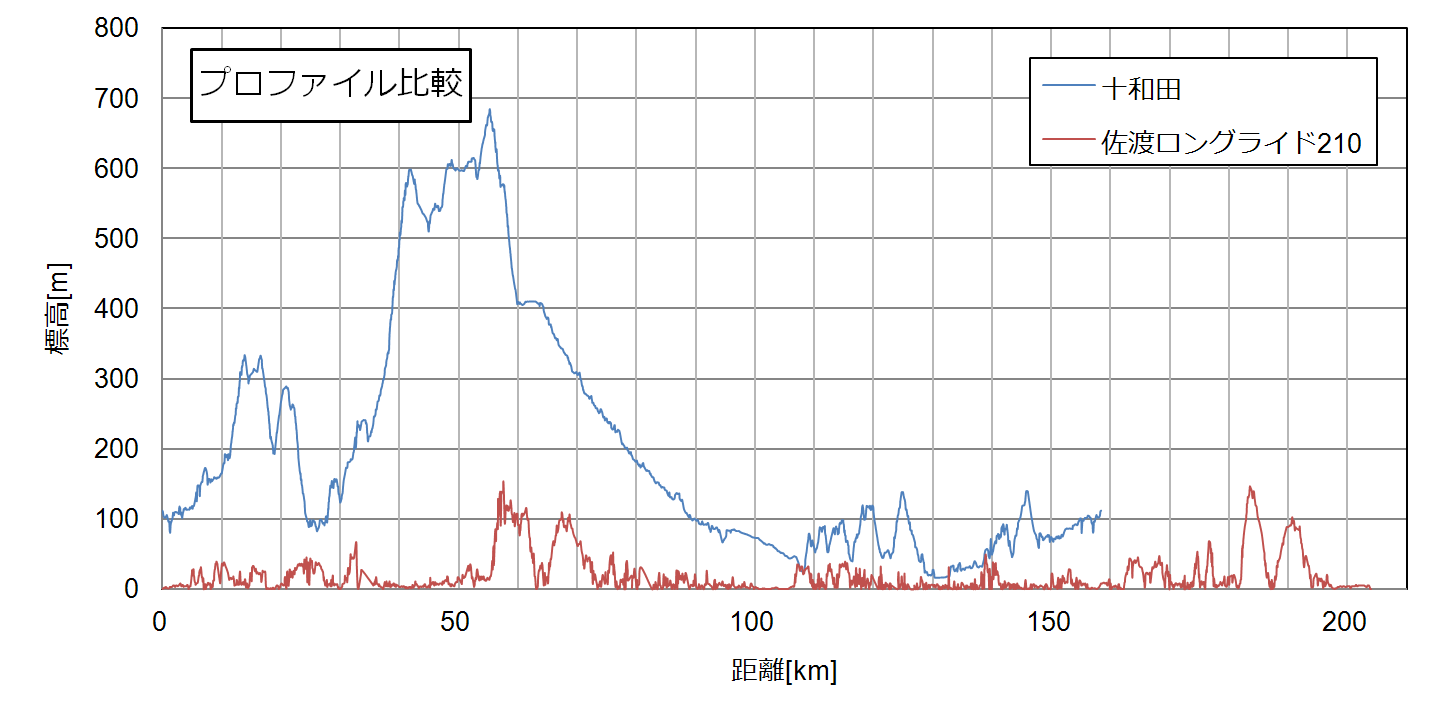
距離にしても獲得標高にしても、佐渡の7~8割程度という結果になりました。
でも、なんとなく、プロファイルを比較すると今回のコースは佐渡より負荷(傾斜)が厳しいような印象も受けます。本当に今回のコースはそれほど軽いものなのでしょうか。
も少し詳しく調べてみたくなりました。
やり方としては、コース傾斜の分布を調べるというものです。コースを単位区間に区切り、それぞれの区間における平均傾斜を求め、傾斜の範囲と量を定量化します。
まずはコースのプロファイルデータを作成します。
これは、ルートラボの GPX データから求めるのが簡単です。具体的には
 |
このとき、GPX データは XML テーブルとして開きます。
 |
lat は緯度(latitude)、lon は経度(longitude)、ns1.ele は標高(elevation)。
一行がひと組の "緯度-経度-標高" データに相当します。
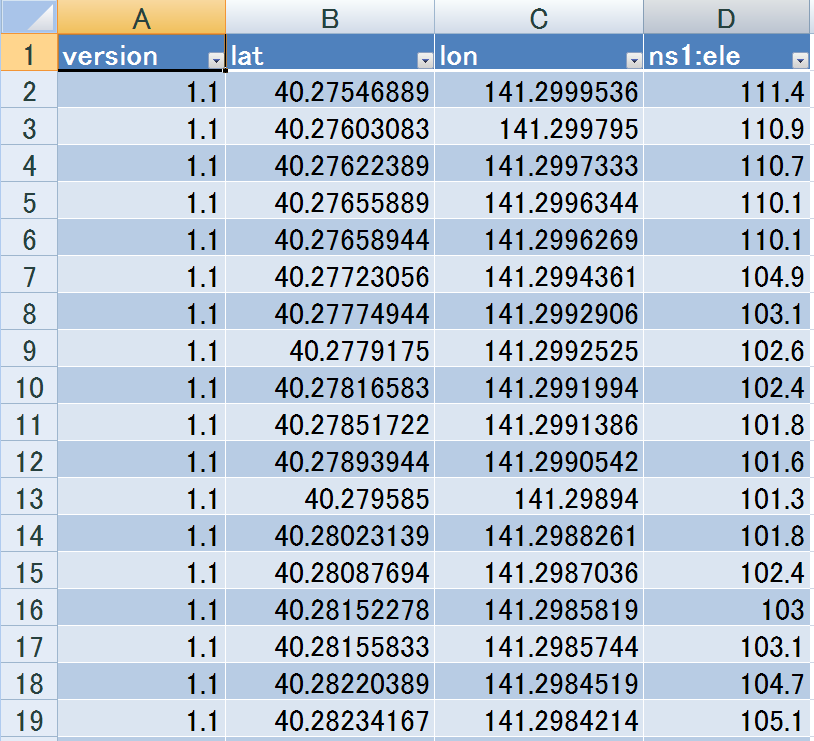
地球上の2地点間の距離の求め方は、計算サイト参照。
ここで、F3セルの数式は
"= 6378.137*ACOS(SIN(B2/180*PI())*SIN(B3/180*PI())
+COS(B2/180*PI())*COS(B3/180*PI())*COS((C3-C2)/180*PI()))"
としました。これは2行目と3行目の "緯度-経度" 座標間の距離[km]に相当します。
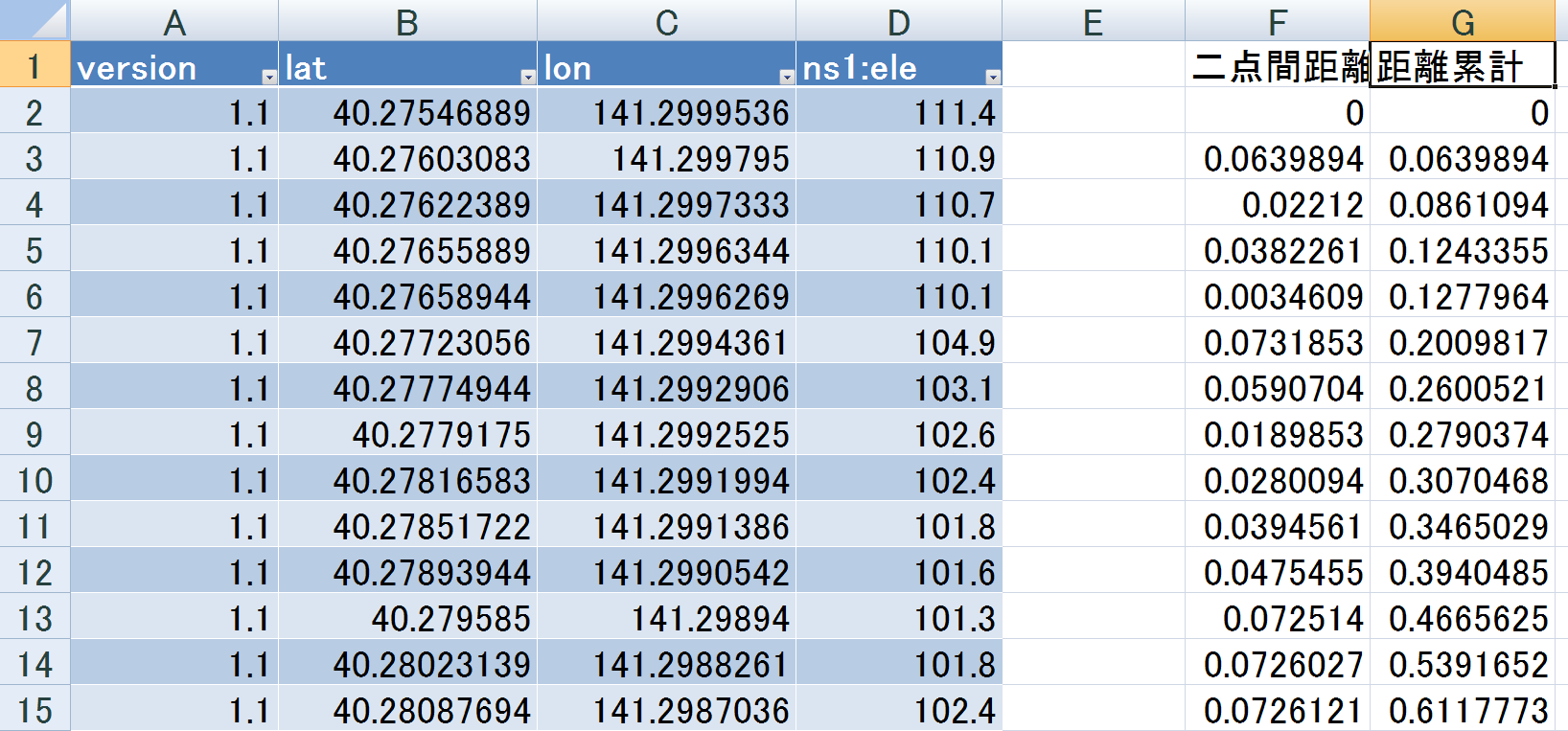
あるいは、以下のようなエクセルマクロを組んだ方が楽かもしれません。この関数を使い、F3セルに "=distance(B2,C2,B3,C3)" と入れれば、上と同じ結果が得られます。
|
Function distance(lat_1 As Double, lon_1 As Double, lat_2 As Double, lon_2 As Double) As Double r_earth = 6378.137 '地球の半径[km] deg2rad = 3.14159265358979 / 180 'degをradに変換するための係数 la1 = lat_1 * deg2rad la2 = lat_2 * deg2rad lo1 = lon_1 * deg2rad lo2 = lon_2 * deg2rad temp = r_earth * Application.WorksheetFunction.Acos(Sin(la1) * Sin(la2) + Cos(la1) * Cos(la2) * Cos(lo2 - lo1)) distance = temp End Function |
F列の累計をG列に入れ、G列(距離累計)とD列(標高)を対比させるとプロファイルデータとなります。
これにより得られた今回のコースのプロファイルを、同様にして求めた佐渡ロングライドコースのプロファイルと比較した結果が、先にも示したこのグラフです。

次に、傾斜を求めます
ここでは 0.5km 単位で傾斜を求めることにします。
G列(距離累計)を見ると、 0 ~ 0.5km は 2 行から 13 行までの範囲ですから、この範囲の傾斜は "=slope(D2:D13,G2:G13)/1000" となります。
同様にしてコース全体の 0.5km 刻みの傾斜を求めた結果がこちら。
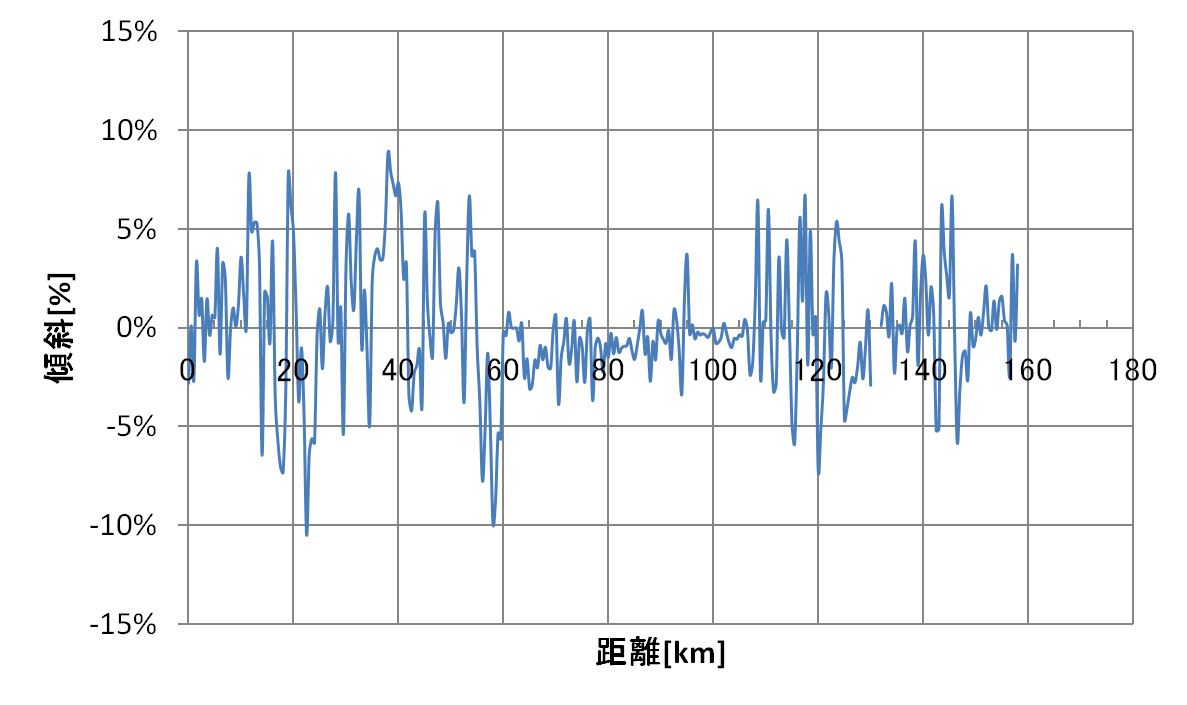
なんだかごちゃごちゃしていて判りにくいですね。
なので、いろんな傾斜がどの程度現れているかをヒストグラムというグラフにまとめてみることにしました。
「ヒストグラムって何?」と言う人は、Wikipedia を参照してみてください。ここでは「どの程度の大きさの傾斜が、どの程度の数出現しているか」を示します。
結果はこちら。
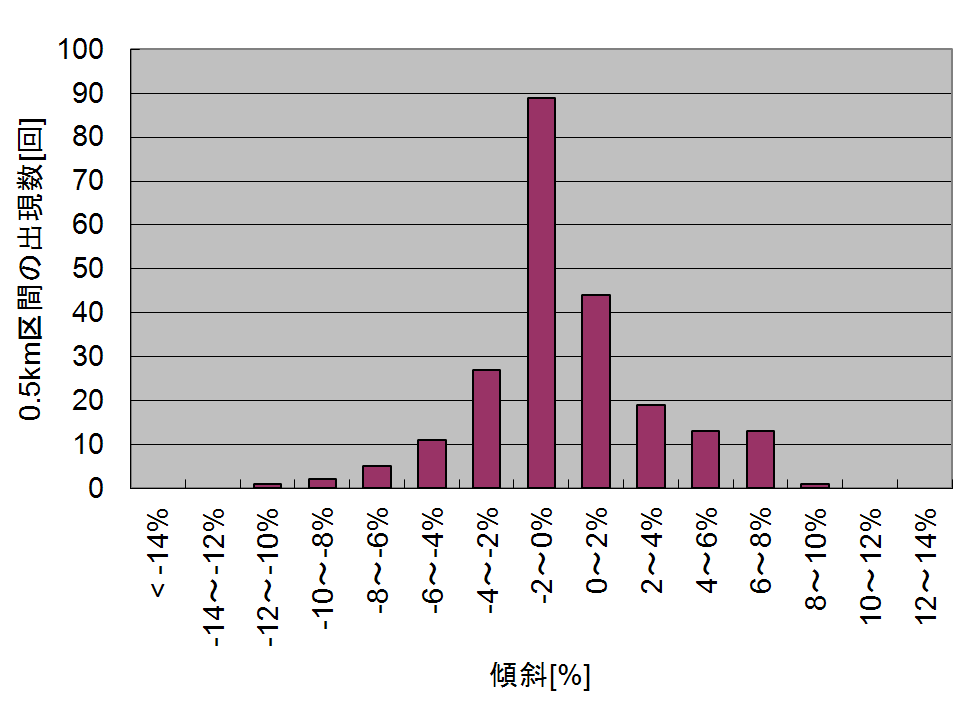
今回走った十和田-奥入瀬コース中最も多かったのは 0~2% の下り勾配で、その数は 89 回でした。ちなみにここでは 0.5km 単位での出現回数を求めていますので、距離に直すと 89[回] × 0.5[km/回] = 44.5km になります。
そして佐渡ロングライドのコースと比較した結果を下図に示します。ここでは判りやすくするため、縦軸は "出現回数" から "距離" に変換しています。
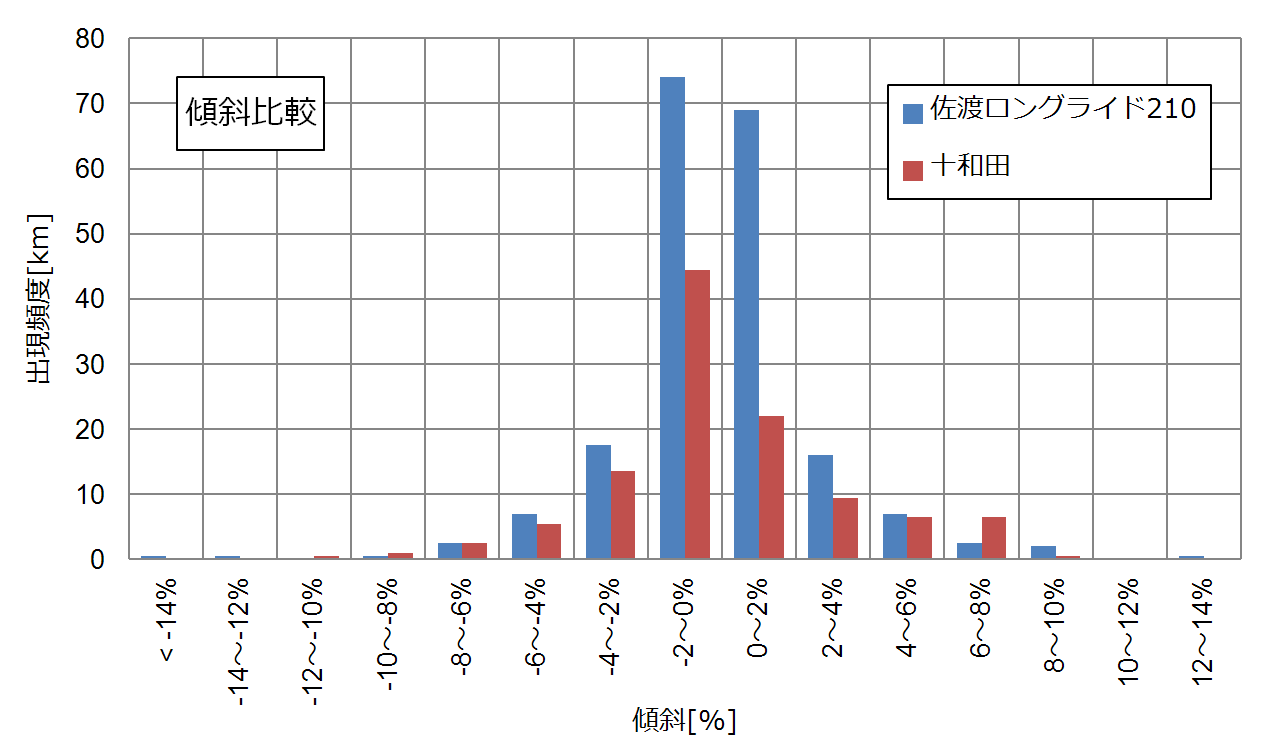
こうしてコースの傾斜と頻度をヒストグラムにまとめることで、全体的なコース傾斜の傾向が判りやすくなったように思えます。
佐渡ロングライドのコースはその大半が -2~2% 傾斜の範囲に収まっています。しかし正負最大傾斜の幅は広く、+12.8% ~ -14.6%もの開きが有ります。つまり言い換えると「佐渡ロングライドコースの大半は平坦路だけど、ごく稀に急傾斜の坂が現われる」ということなのでしょう。
一方で、今回走った十和田のコースは、佐渡ほど平坦路/急傾斜の比率差は極端では有りません。コース全体の距離は佐渡ロングライドコースの 77% 程ではありますが、4~8%傾斜の出現(距離)数は佐渡とほとんど変わらないくらいです。
なので、4~8% の坂を対象としていたのであれば、今回のコースは良い練習になったのだろうと思います。一方で「長い平坦路を速く走る」とか「12% を越える坂を上れるようになる」という目的であったとしたら、今回のコースは不適当だったのでしょう。
...などとつらつら考えているうちに、山路を上り切り峠に着きました。眼下にはかすかに湖面が見えます。ここを下れば十和田湖のようです。
このツーリングを終え家に戻ったら、今考えたようなやり方でコースの比較をしてプライベートランレポートに載せてみようか、などと思いました。
| 2012年08月 十和田湖、奥入瀬 |
■トップへ戻る |